Back

From Chapter 1.

Chapter 1 Question 9.  Scientific notation
a) 100 million = 100 x 10⁶ = 1 x 10⁸
b) 80,000 = 80 x 10³ = 8 x 10⁴
c) 7/1000 = 7 x 10^-3
d) 35 billion = 35 x 10⁹ = 3.5 x 10¹⁰
e) My age 3.1 x 10¹
f) Numbered pages in book, not including front matter 8.23 x 10² (at least Prof.'s version)

Chapter 1 Question 10.  Units
a) km = kilometer [= 1000 meters]
b) cm = centimeters [= 0.01 meters]
c) s = seconds
d) km/s = kilometers per second
e) mi/hr = miles per hour
f) m = meters
g) m/s = meters per second
h) h = hour
i) y = year
j) g = grams (formerly gm)
k) kg = kilograms [= 1000 g]

Chapter 1 Question 11.  Procyon is 3.5 pc (parsecs)  from Earth
a) 3.5 pc = 1.08 x 10¹⁴ km
b) light takes 11.42 years to get from Procyon to Earth

Chapter 1 Question 23.  Small angle formula

Suppose your telescope can give you a clear view of objects and features that subtend angles of at least 2 arcsec.  What is the diameter of the smallest crater you can see on the moon.

D = ad/206,265 (page 13 in book)
        a = 2 arcsec
        d = 384,000 km (pg 13 and 66)
D = (2 arcsec)(3.84 x 10⁵ km)/206,256
D = 3.72 km

From Chapter 2.

Chapter 2 Question 7.  Basic angles
What is the angle between the horizon and the zenith: 90 degrees

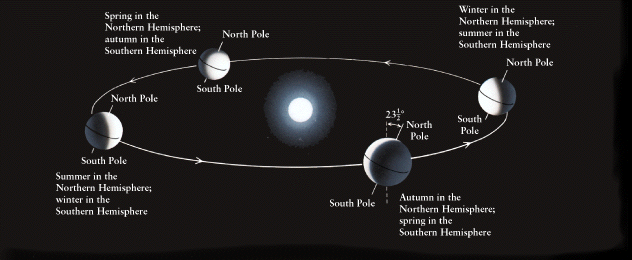
Chapter 2 Question 10.  The seasons
The Earth's axis is tilted 23.5 degrees relative to the plane of its orbit around the Sun.  Furthermore, the axis generally points in the same direction (neglecting procession of the pole).  Therefore, as shown in the figure, there are times in the Earth's orbit when the northern hemisphere is tilted towards the sun (summer) and times when it is tilted away.  When tilted towards the sun, the northern hemisphere gets more direct sunlight (primary cause for summer warming) and the days are longer (secondary cause for summer warming).

Chapter 2 Question 24.  Sidereal motions
On Dec 1, 10:00 pm, Procyon is rising (its on the eastern horizon).
Method 1:  Geometry
    Two weeks later, on Dec 15, the Earth will have moved 14/365ths of the way around its orbit, or 13.8 degrees (counter clockwise).  Since we measure time relative to the Sun, the eastern horizon will be pointed 13.8 degrees further east in the celestial sphere.  In other words, Procyon will already be 13.8 degrees above the horizon at 10:00pm.  It takes 13.8 degrees/360 degrees * 24 hours = 0.91 hours to go 13.8 degrees, so Procyon rose 0.91 hr * 60 min/hr = 55 minutes earlier, or at 9:05 pm.

Method 2: Sidereal time
    Procyon rises at the same sidereal time every day.  A sidereal day is 23^h 56^m 4.091^s.  That means the star rises 3^m 55.909^s earlier every solar day.  Lets convert this to minutes so the math is easier 3^m + 55.909^s/60 s * 1 min = 3.932 min.   In 14 days, the sidereal day has fallen 14 * 3.932^m = 55.05^m behind, or Procyon rises at 9:05pm
 

Chapter 2 Question 30.  Solar elevation at 40 degrees latitude on winter solstice

At the winter solstice, the sun is 23.5^o below the line extending from the center of the Earth to the equator (the northern hemisphere is tipped back).  I am 40^o north of that line.  Therefore, the angle between my zenith  and the sun is 23.5^o + 40^o = 63.5^o (see figure).  The question asks for the the angle of the Sun above my southern horizon.  This is just 90^o - 63.5^o = 26.5^o.

Note, when drawing figures of the Earth and moon where you want to show angles, it is handy to use the fact that the sun (or the solstice/equinox points) are very far away.  That means a line from any point  on your drawing to the sun is parallel to the line extending from any other point on your drawing towards the sun.

From Chapter 3.

Chapter 3 Question 3.  On the vernal equinox, what is the phase of the moon if it is located at
a) vernal equinox -- new
b) summer solstice --1st quarter
c) autumnal equinox-- full
d) winter solstice -- last quarter

To picture what is going on here, it is helpful to draw two figures.  First, the motion of the earth around the sun with the points of the equinoxes and solstices labeled:

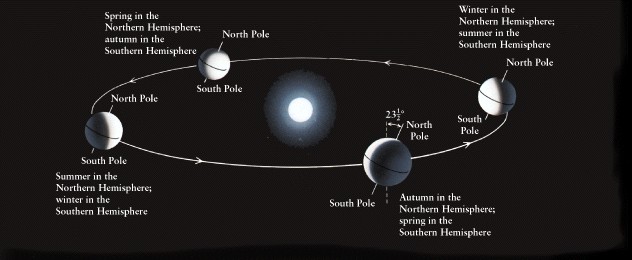
This figure establishes the directions to the equinoxes and solstices.  Yes, you can think of them as specific points on the sky, but they are so far away that they end up just defining directions, like the points of a compass (see note in the solution of chapter 2 question 30).  Be careful not to get the directions mixed up.  They point TOWARD the SUN at the time in question.

Chapter 3 Question 6.  Sidereal and Synodic months
The difference between sidereal and synodic month is analogous to the difference between sidereal and solar days.  A sidereal month is the length of time it takes for the moon to make one complete orbit around the earth with respect to the stars.  A synodic month is the length of time it takes for the moon to orbit with respect to the sun.  This is also the amount of time it takes the moon to complete its phases.  The figure shows that because the earth moves around the sun in the same direction as the moon moves around the earth, the synodic month is longer.  Starting the months at the same new moon, the point of completion of the sidereal month happens before the completion of the synodic month.

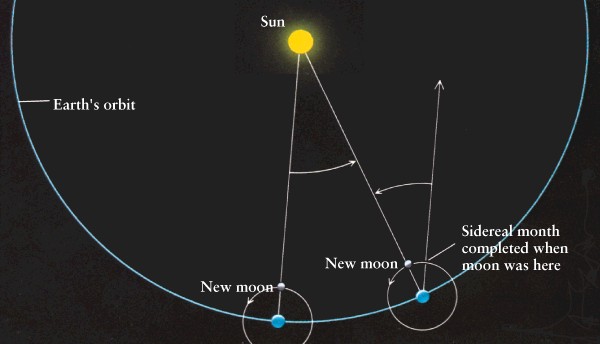
Chapter 3 Question 21.  Retrograde moon

If the moon orbited in the opposite direction than it does but at the same speed, the synodic month would be shorter than the sidereal one.  This can be seen in the above figure, since if the moon goes clockwise, it will hit the "new moon" point before the point at which the sidereal month is complete.

Chapter 3 Question 28.  Jupiter's angular size.
If it takes 90 seconds for the Moon (our moon) to occult Jupiter and the moon and Jupiter were lined up so we can ignore effects of the curvature of the Moon, we can find the effective angular diameter of Jupiter if we know the moon's angular speed.  The problem states we should assume Jupiter doesn't move during this time.  This is a hint that we should use a sidereal month to find the moon's angular speed.  After all, we don't want to know how much the moon's phases change in 90 seconds, we want to know how much it has moved in angle relative to background objects.

1 sidereal month = 27.3 days
1 sidereal month = 360 degrees

The book suggests that we use seconds and arcseconds
27.3 days x 24 hr/days x 60 min/hr x 60 s/min = 2358720 s
360 deg x 60 arcmin/deg x 60 arcsec/arcmin = 1296000 arcsec

Notice how when converting units, all of the intermediate units must cancel properly

Now we have the necessary ingredients to answer the problem using ratios.

1296000 arcsec / 235872 s  =  ? / 90 s

Where ? is the angular diameter of Jupiter, which works out to be:

1296000 arcsec / 235872 s  x  90 s  =  49.5 arcsec

Back