Back

Chapter 4 Question 8.  Galileo's observations and the heliocentric model
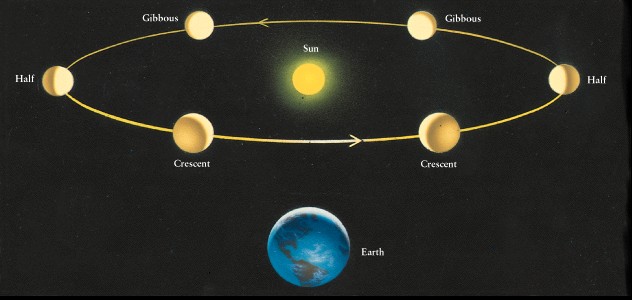
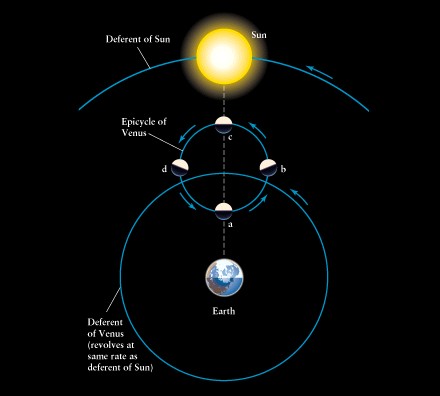
Galileo observed phases of Venus much like phases of the moon.  In particular, he saw a gibbous Venus.  A gibbous phase is only possible if Venus goes behind the Sun, which is predicted in the heliocentric model.  In the Ptolemaic system, Venus is always in front of the Sun and is therefore always in crescent phase.

Textbook Figure 4-14: Heliocentric model

Textbook Figure 4-15: Ptolemaic model

Chapter 4 Question 12.  Satellite around the Sun
P² = a³ P in years, a in AU
Perihelion = 0.5 AU
Aphelion = 3.5 AU
Major axis = 0.5 + 3.5 = 4 AU
Semimajor axis = a = 2 AU
P = sqrt(a³) = 2.8 years

Chapter 4 Question 16.  Force of gravity between earth and moon

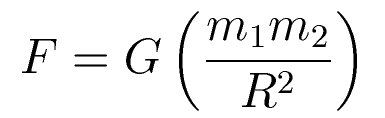
G = 6.67x10^-11 Nm²/kg²
m₁ = 7.35x10²² kg
m₂ = 5.98x10²⁴ kg
R = 384,400 km = 3.844x10⁸ m

F = 1.98 x 10²⁰ N

The Sun-Earth force is 3.53 x 10²² N, or 178 times stronger.
 

Chapter 4 Question 26.  Geosyncrhonous orbit
(a) To stay over the same place on earth, the satellite must orbit at the same rate the Earth turns -- once every 24 hours.  A slight adjustment to this is the fact that 24 hours is a mean solar day and we would count one full rotation of the satellite with respect to the background stars, or the sidereal day: 23^hr 56^m 4.091^s.  Since the book's answer is 24 hours, lets count either as OK.

(b) How big is the orbit?  I intended this to be solved with Newton's form of Kepler's 3rd law.  Unfortunately, I never told you the units of Newtons can be broken up into kg m/s².  This probably made it hard for many of you to get the units right.  Also, though I happen to know most satellites have masses around 1000 kg, most of you probably don't.  However, you might have been able to guess that any satellite is very small compared to the Earth, so when added to Earth's mass in the formula, it doesn't make any difference.

Or about 11% of the way toward the moon.

Another way to solve this problem is to use P² = a³ but express instead of using units of years and AU, as for the case of objects around the Sun, use sidereal months and trhe distance between the earth and moon.

(c) The orbit of the satellite lies in a plane.  If that plane is inclined relative to the plane of the equator, the satellite will move north and south along a longitude line.

Chapter 4 Question 28.  Weight on Mars.
Appendix 2 gives the answer in the surface gravity column: you would weigh only 38% of what you would on Earth.  Another way to solve this question is to calculate the force of gravity you feel on Earth and on Mars.  The force of gravity is defined as your weight.

or F = 980 N.

You can apply the same formulae to Mars (using the diameter and mass listed in Appendix 2):

or F = 370 N.  The ratio of your weights on the two planets is (370 N)/(980 N) or 38%.

Chapter 5 Question 1.  How many times does a light beam travel around the Earth in one second?

That means we need to know the circumference of the Earth.  The diameter of earth is d = 12756 km.  Circumference, pd = 40074 km or 4 x 10⁷ m.  What we want to know is how many circumferences light travels in one second.  We can do this as a units problem:

1 circumference = 4 x 10⁷ m
c = 3 x 10⁸ m/s
c = 3 x 10⁸m/s / (4 x 10⁷ m/circumference)
c = 7.5 circumferences per second.

Light goes around the Earth 7.5 times in one second.

Chapter 5 Question 4.  Wavelength to frequency: n = c/l
c = 3 x 10⁸ m/s
l = 825 nm = 8.25 x 10^-7 m
n = 3 x 10⁸ m/s / 8.25 x 10^-7 m
n = 3.64 x 10¹⁴ Hz
Compare to the clock speed of your computer: 400 x 10⁶ Hz.

Chapter 5 Question 5.  Frequency to wavelength, n = c/l
c = 3 x 10⁸ m/s
l = ?
n = 89.9 Mhz = 8.99 x 10⁷ 1/s
l = c/n
l = 3 x 10⁸ m/s / 8.99 x 10⁷ 1/s
l = 3.37 m

Chapter 5 Question 12.  Rutherford's experiment in 1910 showed that some energetic particles bounced when they were aimed at gold foil.  Since the average density of the foil was not high enough to deflect the particles, Rutherford concluded that there must be very dense particles in the gold foil.  He called these particles nuclei.  in order for the average density to work out, the rest of the foil must be mostly empty space.

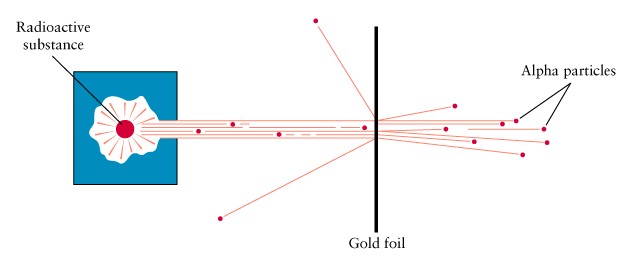
Chapter 5 Question 24.  Absorption lines and chemical content
The wavelengths 588.99 nm and 589.59 nm can be found on the energy level diagram on page 123 of the textbook.  This is a diagram for sodium (Na).  The presence of these lines in the sun's spectrum shows that there is sodium in the sun.  In particular, since we see the lines in absorption, the sodium must be part of the cooler, outer parts of the sun's atmosphere through which the rest of the sun's light shines.

Chapter 5 Question 25.  Energy to wavelength
E = hv (think sneeze)
n = c/l (from book)
E = hc/l
l = hc/E
h = 6.625 x10^-34 J s = 4.135 x 10^-15 eV s
c = 3 x 10⁸ m/s
E = 511 keV = 5.11 x 10⁵ eV
l = (4.135 x 10^-15 eV s) (3 x 10⁸ m/s) / (5.11 x 10⁵ eV)
l = 2.43 x 10^-12 m = 2.43 x 10^-3 nm
This is very short wavelength radiation compared to optical light which is 400--700 nm.  These 511 keV photons are X-rays.

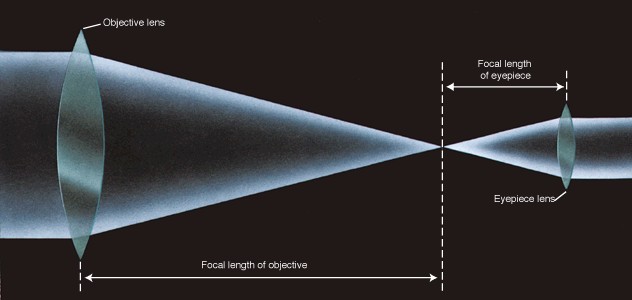
Chapter 6 Question 2.  Refracting telescope
A refracting telescope uses two lenses to collect and magnify light.  The objective lens has a large diameter, the eyepiece lens a small diameter.  The objective and eyepiece lenses are positioned relative to each other so that the image formed by the objective lens falls at the focal point of the eyepiece lens.

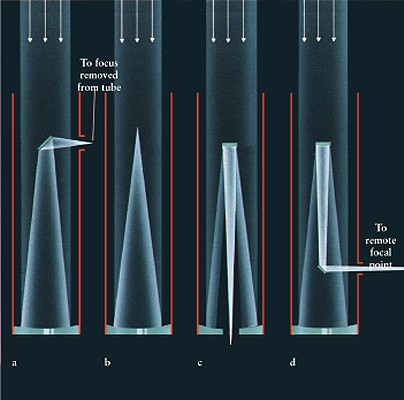
Chapter 6 Question 4.  Reflecting telescope
A reflecting telescope is similar to a refracting telescope in that two focussing elements are used.  In the case of the reflecting telescope, the first element is a curved mirror instead of a lens.  The eyepiece of a reflecting telescope can be at the focus of the primary mirror (prime focus--panel b in figure), but such a the telescope would have to be very large.  To avoid having the observer block the incoming light, a Newtonian telescope uses a small mirror to divert the light (panel a).  An variation on the Newtonian design in the Cassegrain focus, which aims the light through a hole in primary.  An additional mirror can be added to a Cassegrain arrangement to beam  the light out of one of the rotation axes of the telescope. This is a coude focus arrangement (panel d).

Chapter 6 Question 13. ' Windows' in the atmosphere
The optical and radio windows refer to regions in the electromagnetic spectrum where the atmosphere is transparent. The atmosphere is opaque to X-ray ultraviolet radiation, so there are no 'windows' for these wavelengths.  These wavelengths must be observed from above the atmosphere.

Chapter 6 Question 15.  Upside-down images
Using the figure for chapter 6 problem 2, note that the beams of light from the top and bottom of the objective lens cross at the focal point of the lens.  Thus a portion of the image that was above another portion of the image is now below it.  In other words, the image is now upside-down.  The same effect can be observed with a magnifying glass: hold the lens close to your eye and gradually move it away.  At first the image is right side up.  Then, at a certain point, the image flips.

Back