Back

From Chapter 18.

Question 2.  The three layers of the Sun's atmosphere are the photosphere, chromosphere, and corona.  The photosphere is where most of the visible light from the sun appears to originate.  Its average temperature is 5800 K.  Like Earth's troposphere, the photosphere gets cooler with altitude, so it has an absorption line spectrum.  The chromosphere is much less dense and, on average, hotter than the photosphere.  It has an emission line spectrum with H-a as the dominant line.  The corona is hotter still and extends several solar radii into space.  The corona forms the base of the solar wind.  Because the chromosphere and corona are much less bright than the photosphere, they are only visible during solar eclipses or with special instruments.

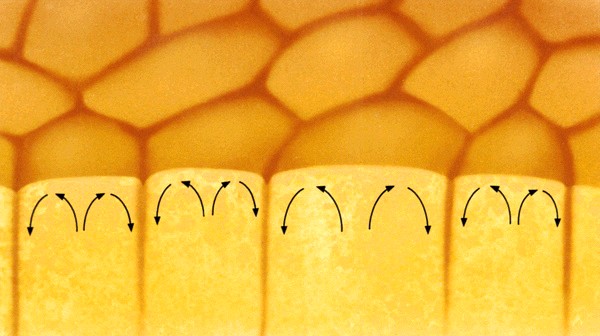
Question 3.  Granulation
The photosphere is broken up into thousands of convection cells.  Each cell appears brighter in the center than on the edges, hence, together the cells look like grains of sand.  The brighter central region of a granule formed by hot material rising through the photosphere.  When the material reaches the surface, it cools, is pushed out to the edge of the granule and falls back down.  In a moving picture, the granules appear to seethe, as their boundaries push against each other.

Question 13.  Hydrogen burning
Hydrogen "burning" is a nuclear process in which four hydrogen nuclei (protons) are combined to form one helium nucleus (two protons and two neutrons).  The because the mass of the helium nucleus is less than the combined mass of four protons, the process releases energy according to Einstein's equation, E=mc², where m is the mass difference.  "Burning" in the strictest use of the word refers to chemical reactions where chemical bonds (formed by electron orbits around atomic nuclei) are rearranged and is not a nuclear process at all.

Question 18.  Density of the sun

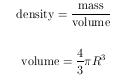
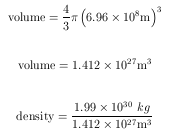
Question 24.  Measuring sun's rotation from Earth.
Sunspots provide a fixed point on the surface of the sun which can be used to observe its rotation.  If the Earth remained fixed in space, by observing a sunspot return to the same place in the disk of the sun, one could measure the period of rotation of the sun.  However, since the Earth moves around the sun counter-clockwise, the sunspot will actually appear slightly to the left of its starting point when the complete rotation of the sun is finished.

Question 25.  Mass-energy conversion, E = mc²
c = 3 x 10⁸ m/s
a) m = 2 x 10^-26 kg  E = 1.8 x 10^-9 joules
b) m = 1 kg               E = 9 x 10¹⁶ joules
c) m = 6 x 10²⁴ kg   E = 5.4 x 10⁴¹ joules
 
 

From Chapter 10.

Question 1.  When to observe Mercury
Because Mercury has such a small orbit, it never gets far from the sun.  Hence, for naked eye observations, you can only see Mercury close to sunrise or sunset.  Telescopes with special filters, however, can see Mercury in broad daylight.  In order to avoid distortion from the atmosphere, it is best to observe Mercury with a telescope near noon, when Mercury and the sun are both high in the sky.

Question 3.  Mercury does not have a substantial atmosphere because it is small and hot.  Being small, it doesn't have very much gravity, so gas escapes easily.  Being hot, any gas molecules that are present move very quickly and are likely to escape Mercury's gravitational field even if they would otherwise be bound to Mercury.

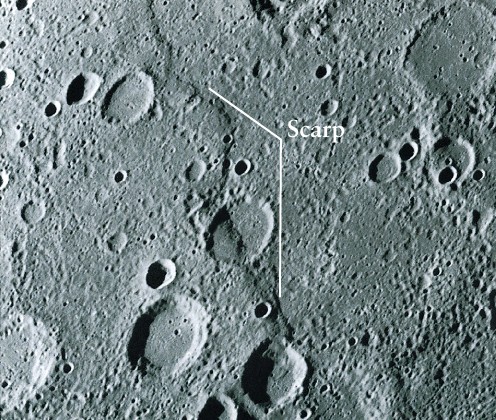
Question 9.  Mercury does not have tectonic features caused by motions of large parts of its crust.  However, parts of Mercury's crust have slumped relative to others, probably as a result of the contraction of the planet as it has cooled over its lifetime.  These features are probably old compared to Earth's tectonic features (which are still happening today!) because they are dotted with many craters.

Question 21.  How much would an 80 kg person weigh on Mercury?
Recall from the solution of chapter 9 question 18 in homework #3  that there are two ways to solve this problem.

Method 1: First of all what does an 80 kg person weigh on the Earth?  Weight is the force of gravity, F = ma, where a = 9.8 m/s² on the Earth.  Thus, 80 kg weighs 80 kg x 9.8 m/s² = 784 kg m/s², or 784 Newtons.  The surface gravity of Mercury is 0.39 that of Earth's (table 10-1), so 80 kg weighs 784 N x 0.39 = 306 N.  The moon's surface gravity is 0.17 that of Earth (table 9-1), so 80 kg weighs 133 n on the moon.

Method 2: Newton's universal law of gravitation.  Let's mass produce the answers by calculating the quantity Gm₁/R² for each body.  Then we can multiply by whatever m₂ we want (80 kg in this case)

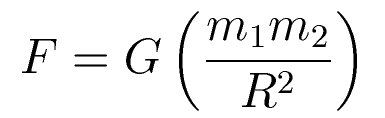
Note, because of Mercury's slightly oblong shape, its average surface gravity and its equatorial radius give slightly different answers.  The true answer depends on exactly the 80 kg person is standing.

Back