Back
 Next
Aristarchus & the Size/Distance of the Sun and Moon:

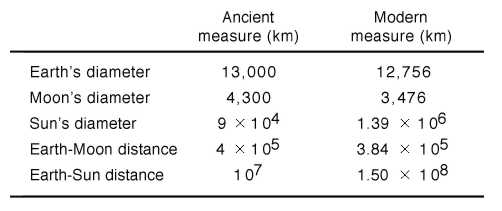
An earlier Greek astronomer, Aristarchus, had already provided a means by which Eratosthenes' discovery could be used to get the distances to the Moon and Sun, as well as their diameters.  To do this you must use the Moon.

He used 2 tricks:

1)    First, he used the basic geometric principal that the Sun, Moon, and Earth form a right triangle when the Moon is at quarter phase.







By measuring the angular separation of the Sun and Moon at the exact instant of the quarter moon phase, you can derive the relative distances of the Sun and Moon!!! (use the Pythagorean theorem)

His measurement was that the angle between the Sun and Moon was 87° which implied a ratio of 20:1 for the relative distances to the Sun and Moon.

As it turned out, this was a very hard measurement to make, because the true ratio is more like 400:1.  Aristarchus would have had to measure the Sun-Moon separation to within 0.15° to get it right; a daunting task.

The other number Aristarchus tried to determine was the Diameter of the Moon, which he did a better job with.  To accomplish this, he measured how long it took the Moon to traverse the Earth's shadow during a Lunar Eclipse.

Using this time he concluded that the Moon was 1/3 the Earth's Diameter.

He also extrapolated this result to the Sun.  By noting that the Sun and Moon were the same angular size but with a distance ratio of 20, he claimed that the Sun was 20x larger than the Moon, or 7x larger than the Earth!  This was a good guess, but it is also limited by his inaccurate measure of the relative distances that is described above.


Back
 Next